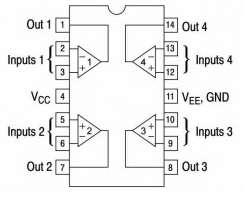
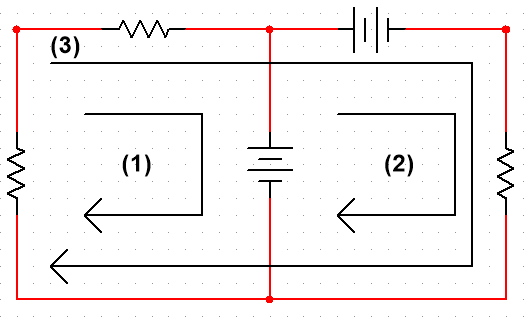
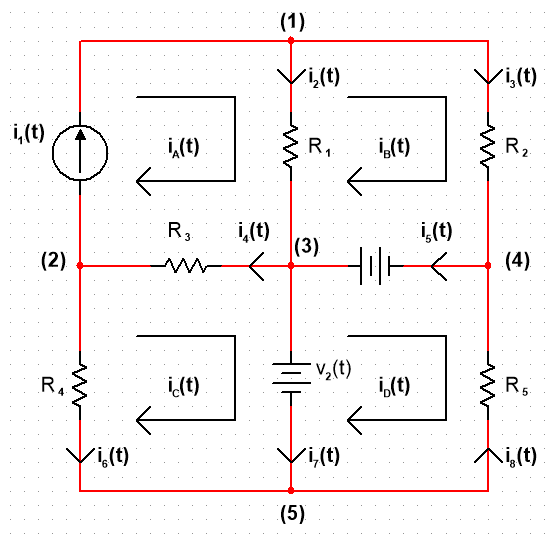
회로 설계하기 다음과 같이 주어진 출력이 되도록 두 입력 V1과 V2가 있는 op-amp 회로를 설계한다고 했을 때, 설계하고자 하는 출력 방정식 주어진 방정식은 표준형 차동 증폭기의 출력이다. 아래와 같은 회로를 사용한다고 해보자. 그럴 경우 이 회로망의 출력 방정식을 나타내어 위의 주어진 출력 방정식과 비교하면 된다. 회로의 출력 방정식 각 입력 전압 V1과 V2의 계수와 비교하여 구하도록 한다. 따라서, R1 = 10kΩ, R3 = 20kΩ 으로 선택한다고 하면 R2 = 50k,Ω R4 = 30kΩ이 된다. 두 번째 회로에서 계측 증폭기는 프로세스 제어 또는 측정 분야에 사용되는 미세 신호의 증폭기이고 단일 패키지 단위로 시장에 사용화되어 있다. 이 회로에서의 출력은 어떻게 나오는지 해석해보도록 하..